Introduction
-
The goal of this work is to develop a set of methods for showing that large programs possess important control flow properties. The properties of interest are those related to the continued operation of programs in the face of particular residual faults in the program implementation. These faults can affect the program's compliance with aspects of its specification, and it is therefore desirable to be able to show that classes of these faults are not present and/or cannot affect the program adversely.
-
The intended approach is to embed specifications for program operations inside of the program implementation. The specifications are written in a limited formal notation and serve to describe important properties of the operation in a parseable form. Particular properties of conformance between the specification and the implementation of the program will be mechanically verified before the executable form of the program is permitted to be created.
-
The final version of the program, including the final source code and the final executable program, is synthesized using the specifications and source code provided for the program. These are combined with a special set of code fragments (written using the target language) by a translation tool. The fragments will be shown to possess certain desirable control flow properties of their own and will serve as the internal structuring method within the synthesized program. Given a certified compiler that generates code conforming to the language definition for control flow, the programs created by the translator will possess particular desirable control flow properties.
-
The current set of properties that are considered important are stated negatively; the verification system will prove that particular situations do not exist within the program. These situations are members of a compendium of anomalies that have been found to have adverse effects on continued or appropriate program operation. One anomaly can cause an Ada program to deadlock with one of its tasks. Another anomaly can cause a memory leak in C++. The precise description of each anomaly can be a mixture of language dependent and language independent statements.
-
The thesis of this research is that a process exists for developing operations such that the operations are total and, while remaining cost effective to specify and implement, the operations developed this way can have certain of the properties of importance verified for them. To determine the validity of the thesis, a set of experiments will be carried out to build libraries of total operations and programs based on the libraries. These code artifacts will be the basis for analysis, verification and testing, and will help to establish the proof of concept.
mini-index of document
-
The remainder of the document is organized as follows.
Literature Basis
-
<use only present tense>
-
Many languages and environments offer exception handling mechanisms; for example, Ada [], C++ [], Mesa [], Clu [], Mach [] and PL/I []. Some specification languages also deal with the issues involved in exception handling; for example, VDM [], Anna [], Denotational Semantics [], and Z []. Numerous authors also contribute to the theoretical basis for exception handling and to advancing the current models available. This section does not attempt to pay homage to all of these contributions, but rather focusses on the authors whose research has had a direct and important impact on the research. A lengthier review of the literature can be found in (appendix???).
-
This research is a logical extension of the research of others in the fields of exception handling and verification. The research attempts to build upon these works and use existing techniques within the context of a set of parsing and verification tools, hopefully bringing these formal techniques into reach of non-formalist programmers and developers.
-
Exception handling semantics are not the only focus of this work; the more general focus is on operation connectivity, or the patterns used for the flow of control and data within programs. In particular, the focus is to be on single-thread connectivity, where only one active computational engine is transforming the program. Functional semantics are included under the connectivity banner--a functional model has a single method for flow of control.
-
The justification for this slightly expanded focus is that the model for total operations attempts to reconcile two major streams of thought regarding exception handling; the for and the against schools. The against school says that exception handling is somehow fundamentally bad and should be avoided. The for school says that exception handling is necessary and natural. An approach to reconciling these two viewpoints is discussed below, after the essence of each of the viewpoints is presented.
-
Dijkstra predates the theoretical development of exception handling, but his early work echoes throughout the subsequent approaches to formalize the field. He develops the notion of describing the input/output relationships intrinsic in program operations with preconditions and postconditions in []. The preconditions describe properties of the operands that the operation absolutely requires to be true for its successful completion. Failure of a precondition is generally referred to as a situation for which the operation is not defined.
-
The postconditions for an operation describe characteristics of the output of the operation and characteristics of the overall program state which are affected by the operation. They are, in a sense, the intended result of the operation as well as the reason why a programmer would choose to invoke it. When a program operation fails to generate a condition described in its postconditions, this is generally referred to a failure of the operation. Operations can fail due to faults in their implementation [].
The For's
-
A firm member of the for school, Cristian extends the notion of preconditions and postconditions to exception handling semantics []. His approach is to describe an operation as a combination of a normal service with a set of exceptional services. Normal service corresponds to the state described in traditional postconditions. The exceptional services correspond to various failures of the operation in the traditional precondition sense of failure, but also provide a particular exceptional (possibly degraded) service.
-
The activating set of circumstances for the exceptional service is described as an exceptional precondition, and the exceptional service's impact on the output and program state is in turn described by an exceptional postcondition. This extension allows exception handlers to be described in terms of their causes and intended actions. Cristian uses his definition of an exception handling operation as the basis for defining robustness; a robust operation is one for which the combination of normal services and exceptional services covers the entire input domain of the operation.
-
<is above correct?>
The Againsts
-
Hoare is a member of the against school.
-
Black follows Hoare's viewpoint that exceptions should not be used []. Black proposes instead using a discriminated union return type within a conventional function call mechanism to simulate multiple exceptions. This approach avoids problems that might arise from the use of two different control flow mechanisms in the program. But problems that arise in verifying that the discriminated union type is used appropriately in the program are very similar to the problems that arise in verifying appropriate treatment of exceptions in the program.
Why Both School's are Right
-
For's are right because the exceptional domain exists. It is pretty traumatic to prove that every single + overflow is precluded by the checks and composed operations of the program. It is not cost effective to remove every one.
-
The Against's are right because once an exception occurs, you are dead in the water in some sense. Why did it occur? Did it definitely occur in the operation that just completed, or was it propagated from some sub-operation? And it is often hard to figure out the exact circumstances under which an exception is raised, since language definitions can be large, confusing, ambiguous or incomplete. If there is no specification for the underlying language operations, there can be no sureness regarding your checks on them.
-
The resolution of this is to first of all stop thinking of the exception as something different from a normal return. It is just another possible outcome from an operation and can be normal in some cases. This allows the "For" school to say "okay, as long as there are multiple outcomes, i agree". The against school will say, well when the heck do these outcomes occur? This requires the exceptions that are possible to be completely described by the underlying language's definition / specification. This allows the "against" school member to say "okay, as long as there are definite conditions under which these occur, then that's okay".
-
is this convincing and right? i don't think the argument holds water yet.
-
-
Other Connectivity Issues
-
Denotational semantics [] deals with multiple exits from operations, such as exceptions, using the continuation. A continuation models the notion of a programming construct that has a non-local flow of control; the construct is passed the "rest of the program" in the continuation, allowing it an exit still described by a functional property, but also not necessarily bound to exit at a single point with a functional value. The continuation allows description of multiple flows of control.
-
Denotational semantics is thus capable of modelling Ada's exception-based operations or the proposed total operation model's operations, and can therefore be used to describe total functions. The point of modelling a program operation with denotational semantics is to establish its formal meaning. The point of using the proposed total operation model is to build software components that possess total operation specifications and to verify properties for these components. The verification aspect is a potential application for denotational semantics, while it is not commonly used as the basis for specifying and implementing a software component.
Proposed Approach
-
The total operation model requires that operations be well-formed syntactically and connectively. Syntactically well-formed refers to how the operation is defined and means that: 1) each operation has a specification, 2) the specification describes formally each service provided by the operation, and 3) the specification details under what exact circumstances each service is provided. Connectively well-formed refers to how the operation is utilized in a program and means that: 1) each of the operation's services is used by some "client" operation, 2) each client's requirements match the service it is being given (as to the type of service, usually limited to agreement in data types), 3)
-
-
The diversity of data types and algorithms virtually requires that methods for ensuring syntactic well-formedness in total operations follow a cookbook approach. These methods will hinge upon showing that an operation's specification describes a mathematical partition of its operand space. A mathematical partition is by definition both mutually exclusive and complete. The current set of methods for ensuring totality includes: 1) spanning an enumeration, 2) spanning ranges, and 3) spanning an axiom set. Spanning refers to the process of making sure every member of a set is accounted for in the specification. To span an enumeration is to ensure that each member of an enumerated type is accounted for (and that illegal enumeration values are not permitted). To span a range is to ensure that a set of ranges covers the entire valid numerical domain of a type (and that illegal values are not permitted). To span an axiom set is to ensure that, when a data type is described by a set of axioms defining the valid values, each element of each axiom set is covered. These methods can serve as the basis for ensuring totality within operations that use the spannable data types.
-
-
Benefits
-
Success in this research can lead to a number of useful results, perhaps both positive and negative results regarding this particular approach to the issues involved in verification of control structures. This section explores a few of the possible benefits.
-
-
<totality is good>
-
The most basic cause for the existence of an exceptional domain is that algorithms are often only partial functions over their operand spaces. This means that the operation is only defined over a proper subset of its input domain. Limiting the operands to the algorithm's standard domain ensures that the algorithm produces a normal result, but when the algorithm is invoked in its exceptional domain, the result is not defined.
partitions represent characteristics of algorithms (hw or sw) or data type's underlying structure
integrated specs
programmer usually concerned with functionality
-
specification slippage can occur
-
reasoning based on specification becomes invalidated with slippage
-
possibly reduce slippage (for some programming tasks based on specification)
-
or eliminate it (for simple aspects of correspondence between spec and implem, such as that a particular number of outcomes are implemented by an operation)
Superiority to Ada without analysis/synthesis
automatic checks on some things programmers commonly forget
-
automatic firewall code for important operations
-
code fragments to be included can be rigorously verified for particular properties off-line, rather than incurring compiler overhead time working on them.
verification
develop methods for totalization
-
develop libraries with some properties verified
-
-
The consequence model embodies a unified mechanism for connecting program operations. This is beneficial because it can be a simplification over the complex behavior exhibited by program with a mixture of procedural/functional returns, exception handling and message passing. The success of the model will hinge largely on whether the features of the model can be provided to the programmer in an elegant and useable form.
-
The consequence model has more connections determined statically within the program than an equivalent program based on exception handling. Exception handling can use a static approach too, or the consequence model could not call upon it to enforce the model. However, in exception handling, the static approach is not an automatic given; one must extremely carefully consider the placement of firewalls and exception handlers in order to ensure this behavior. The consequence model is an advantage over this because most of this detailed structuring is inserted by the translator into the final program. The analysis that would be required every time in the exception handling approach can be done very carefully once for the fragments to be inserted by the translator.
-
Total operations can be a beneficial method for recording important specification information in a form that resides with the program. By forcing the programmer to interact with this specification, it is possible that the specification and the program can be kept synchronized. If the specification and code are separate, it is difficult to make sure that the specification continues to accurately describe the behavior of the program.
Benefits Thoughts
-
what are the most basic levels of benefits here?
-
code improvements? what kind are we offering? maybe enumerate the things the synthesized program can do or will not do: will not have anonymous exception, will not have uncontrolled propagation: require operation at outer boundary and restart? yes, maybe so. will have specification of at least outer level, and will conform to that specification in terms of only terminating by the conseqs in spec. conditions associated with these will be well defined in spec, but the extent possible that we can prove the conformance will be determined. programmer can look at only specification and need only look at the code for bugs?
-
state of the art improvements? are there any totalization things out there? are there any totalization over dynamically allocated data types?
-
code tools will be available for ada users? for c++ users?
-
experience with potential anomalies in ada will be brought to bear on c++ and programs in c++ devd with zeno will benefit?
-
many software libraries exist. several parts from these will be made into total operations at every possible level. these will be available for experiments in verification and may serve as the basis for library components aimed at building large programs with dependable properties underneath as well?
Using Total Operations to Build Hierarchical Subsystems
-
<concisification>
-
An oft-cited reason for the inclusion of exception handling in a programming language is to enhance program modularity by extending an abstraction's responses to program states that violate its pre-conditions []. However, this reason is not valid for Ada because the anomalies often violate the assumption that an abstraction can be implemented by managing only its own concerns. Abstractions in Ada might be forced to manage the exceptions raised in lower-level abstractions without any prior specification of those lower-level exceptions. Anomalies such as uncontrolled propagation and anonymous exceptions can violate the boundaries that are emplaced around an abstraction. The anomalies can make verification difficult even when a program is well-structured.
-
By contrast, operations are defined hierarchically in the consequence model. The basic meaning of this is that no operation can affect its invoker in a manner that has not been specified. Developing enforcement techniques for this strict hierarchical policy is a subject of this research. When this policy is adhered to, there is no situation similar to uncontrolled propagation because all operation consequences must be connected to a successor operation. The notion of exception propagation is different from the notion of connecting consequences; either an operation manages the consequences of the lower-level operations that it invokes, or those consequences are promoted to the specification of the higher-level operation. This decision is made at design time, not at execution time. All consequences of an operation must be considered, either by managing their occurrence inside the operation or by promoting their scope to that of the operation's specification.
-
Hierarchical programs can be implemented using the consequence model. This cannot be claimed for the Ada exception handling model by itself, because the anomalies can cause a violation of the abstraction boundaries in a program hierarchy. Restrictions must be enforced to allow abstractions to be encoded robustly in Ada. As part of this research, it will be determined whether the consequence model embodies the restrictions necessary to allow Ada to serve as an implementation language for truly hierarchical programs.
-
The consequence model can be used to make operations on critical Ada program subsystems into total operations. The main Ada program can control these lower-level systems hierarchically by relying on their specifications. Not all subsystems are necessarily candidates for becoming total operations because of the overhead required to retrofit a total operation model over the Ada programming language. But dependability can still be increased significantly by turning only those subsystems that are particularly critical to the application into total operations.
-
The abstraction A in Figure See Hierarchic vs. Non-Hierarchic Abstractions has a total operation boundary between it and the main program. Each operation on A is defined as a total operation. The arrows represent possible control flows from invoked operations. The operations in abstraction A can only complete by way of the consequences specified for them. On the other hand, abstraction B in the figure is defined in terms of Ada operations. Since its operations are not defined in terms of total operations, any of the operations in B may propagate an unspecified number of exceptions to the Main program. These exceptions are not unknowable, since a static analyzer could determine the full set of propagable exceptions, but at the time of program implementation the programmer does not necessarily know which exceptions can be propagated.

-
Exception handling in existing languages is programmed in a bottom-up manner. While good programmers generally design programs as a hierarchy of abstractions, the semantics for exception handling have no such abstractions. A model used for enhancing program dependability must allow the system designer to specify operations from the top-down []. The overall policy for managing consequences (or handling exceptions) must be visible from the top-level operation of the program, rather than being composed from the interactions within the entire program. To verify the main operation in the second case, the program paths that must be verified can be as long as the entire invocation structure for the whole program. However, when the invoked operations are hierarchical total operations, the paths to verify are only as long as the paths within the main operation itself--the other operations can be independently verified due to their strictly hierarchical nature. The power to implement and enforce adherence to a coherent, top-down policy for control and data flow must be provided, and it seems feasible to provide it within a hierarchical structure.
Iterative Specification Creation
-
<extract iterative allowance as benefit>
-
<extract square root stuff into operation example section?>
-
When an operation is designed, the intended semantics are known before the details of implementation are known. For example, consider an operation that computes the real roots for a quadratic equation. The intended semantics are that it returns either two, one, or no real roots.
-
The intended semantics are not necessarily the same as the actual semantics however; the specification must detail exactly and precisely all factors that can affect the invoker of an operation. On current hardware, arithmetic computations are limited by the size of the largest and smallest representable numbers. Thus the definition of the operation cannot omit the possibility that one or more of the arithmetic operations might overflow or underflow when they are used to solve this equation.
-
Using the consequence model to specify an operation, this recurring situation (where early designs need to interact with real-world computational limitations) is dealt with by introducing a consequence into every initial operation specification: the error consequence. It is called `error' because it is a consequence that signifies that a lower level operation that is not a total operation has completed in an erroneous manner that is not suitable for intelligent handling. This concept has been called a failure exception in the Clu language [].
-
The error consequence arises due to the requirement that operations be total throughout their development process; it serves as the repository for all subsets of the domain that are not covered by user-defined consequences in the earlier stages of program development. The subsets of the input domain might not be covered due to omission, due to resource limitations or due to internal details of the operation's implementation.
-
To see how the error consequence serves as a pivot for refining the specification and implementation of a total operation, consider the quadratic equation example again. If the algorithm for finding the real roots of this equation is taken directly out of a algorithm textbook, it might read something like Figure See Hierarchic vs. Non-Hierarchic Abstractions. This definition of the real_roots function returns an integer that reports the number of computed roots along with an array of real numbers containing the roots.
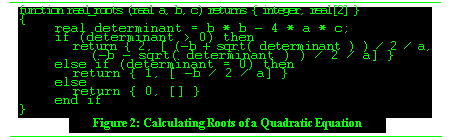
-
The designer might be tempted to simply use this function as an operation by replacing the returned element with three consequences--one for two roots, one for one root and one for no roots. However, in this algorithm, there has been no attempt to describe the expected semantics if an overflow or similar situation occurs. This is commonly the case in programming languages like C that do not have exception handling. Often it is assumed that the parameters will always have ``reasonable'' values and that the operation will thus never encounter situations like overflow.
-
The expression for calculating the determinant is shown in a graphical form in Figure See Hierarchic vs. Non-Hierarchic Abstractions. This figure shows all of the consequences that are left unmanaged by the algorithm as arrows that are not connected to a successor operation. The determinant is produced by this suboperation as the connection between it and the next statement (labelled as a circled `1'). In an ideal world, an addition operation would work for all operands, but in the real world, it will definitely not compute a correct mathematical result when the operands are out of range. Thus, the algorithm in Figure See Hierarchic vs. Non-Hierarchic Abstractions is only a partial algorithm.

-
The computation of the two real roots case is more complex than the determinant calculation, and it also has correspondingly more unconnected consequences, as shown in Figure See Hierarchic vs. Non-Hierarchic Abstractions. As can be seen from these two graphs, there are many cases where the partial operation algorithm will fail to produce an accurate result. Without a multiple-exit mechanism of some sort, the algorithm will not even be alerted when one of the non-standard exits is taken by a mathematical operation. In the programming language C, for instance, the addition operations will just wrap around. The C version of this program would thus compute incorrect values for the two real roots without warning.
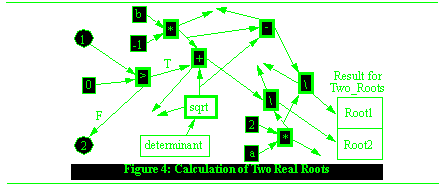
-
Operations specified in the consequence model are not assumed to be invoked with reasonable values. The philosophy held here is that, in general, operations might be invoked on unreasonable values and thus an operation must be prepared for those values. To implement this philosophy, the consequence model automatically maps all consequences without a defined connection to the error consequence.
-
The error consequence's main purpose from an implementation viewpoint is to ensure totality by naively incorporating all segments of the domain that are not explicitly connected by the user. This allows a partial algorithm to form the initial core of an implementation for a total operation.
-
The error's use in the implementation corresponds to its representation as a consequence in the specification. Initially, an operation can be considered to have only one consequence--the error consequence. The operand space is thus partitioned into one equivalence class initially. When a consequence is added to the specification of the operation, previously undifferentiated subsets of the error consequence are covered by the new consequence's outcome specification. When an implementation is provided for the operation, the error consequence begins to acquire a real meaning from the set of unconnected consequences in the implementation. Refinements to the core algorithm might incorporate portions of the error consequence (by supplying connections to previously unconnected consequences) resulting in a change to the specification as well as to the implementation.
-
The initial specification of the non-error consequences cannot be assumed to exactly cover the segment of the input domain that the programmer intends because some of the operations that form the path from operands to a particular consequence might not have all of their consequences connected to successor operations. These unconnected consequences are mapped to the error consequence, and thus each consequence is initially defined as an intersection between its positive domain assertion, such as x > 5, and the negation of the domain covered by the error, in this example
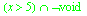 . The error consequence has this `precedence' over the intended consequence specification because the error has a concrete representation while the intended semantics are yet to be proven.
. The error consequence has this `precedence' over the intended consequence specification because the error has a concrete representation while the intended semantics are yet to be proven.
-
The error consequence can assist in proving certain properties for the specification. For example, if the specification of the error consequence completely covers the outcome specification for another consequence, then that other consequence will never occur. This implies that either the consequence is not implemented accurately or that there is no need for it in the specification.
-
In an operation's final form, the error consequence will either serve as a failure interface to the invoker or it will have been completely eliminated. In either case, there are no subsets of the domain that have been left uncovered by the specification. The error consequence is an important part of ensuring that operations are total.
Research Plan
-
The proposed research will be carried out by performing staggered research, development and evaluation stages. The purpose of interspersing these stages is to help to ensure that the action is proceeding in the right direction for achieving successful results. This section describes the milestones to be met in each of the stages.
Research
-
Show Equivalence with Turing Machine
-
Compile a Set of Desirable Control-Flow Properties
-
Prove by Rigorous Argument that These Properties Hold for the Code Fragments
-
Translate Rigorous Arguments into Formal Proofs for Properties
-
Represent Consequence Model in Formal Specification Language
Development
-
Implement Ada parser
-
Implement ZENO translator
-
Implement ZENO Graph Model
-
Implement Example Parts with ZENO
-
Implement ZENO Verifier
Evaluation
-
-
Lower level interfacing
enforce certain characteristics of system use by supplying consequence wrapper
-
how does this affect productivity & reuse?
-
does it assist in stopping errors?
Prove a few interesting properties in examples
heap properties using own heap form
-
all control paths
-
result correctness on a path
development process
guide programmer through process
-
requirements for passing between phases of development
Research Plandendum
-
The overall proposed research is to develop a specification language that supplements the Ada programming language by allowing total operations to be defined, used and verified for important properties. This will involve developing the consequence model more completely and developing the tools to support the model. The primary tools that create Ada programs from ZENO specifications are the translator and the verifier. These are depicted in Figure See Primary ZENO Tools.
-
<the figure is screwed; pull in the nice picture from the defense slides.>
-
<make sure this figure is totally represented in that figure.>
-
<conciser and cleaner and better and morer>
-
The following research goals will be addressed:
An Operation Model Based on Total Operations
-
Development of Total Operation Model
-
Development of Syntax for Model
-
Development of Method of Application of Model
-
Evaluation of approach
Ada Translator for Total Operation Specifications
-
Implement Ada Parser
-
Implement Objects to Support consequence model
-
Implement Dependable Code Fragments Used by Translator
-
Devise Set of Compile-Time Checks for Specifications and their Implementations
-
Implement Interface to Verifier
Property Verification
-
Isolation of Important Application-Independent Properties
-
Provide Syntax for Stating Critical Properties
-
Develop Prototype Verifier
-
Apply Verifier to Existing Ada System for Specified Properties
-
Evaluate Verification Capability
Verifying Programs Based on Total Operations
-
Verifying properties for critical program components is a necessary antecedent to producing dependable software. An operation in the consequence model can be analyzed by tracing each possible data flow path from its operands to each of its consequences. The characteristic predicate for the result produced by each operation invoked on a particular path yields a composite statement of the consequence's result. This composite statement can be entered into a theorem prover to assess whether the specification of the consequence is implemented by the operations composing that path (or group of paths) through the operation.
-
If the implementation of a consequence's result or outcome cannot be proven to conform to its specification, then there are four possibilities:
-
the conformance cannot be proven because the specification is incorrect,
-
the conformance cannot be proven because its proof is impossible,
-
the operation is incorrectly implemented on the path for that consequence, or
-
the available theorems are not sufficient to prove them.
-
To minimize the impact of the first case, specification consistency checking tools could help to locate certain types of incorrectly stated consequence specifications. For example a tool might point out where outcome specifications intersect or where subsets of the domain are not covered. The second case is a possibility given Gödel's incompleteness theorem, but few cases of this sort are expected because operation specifications are usually too simple to induce a logical system of sufficient complexity. In the third and fourth cases, the verification tool should point out the path along which the verification breaks down. The development of more efficient diagnostics for reporting non-verified consequences is a goal of this research.
-
Certain property verifications are necessary in dependable systems. The consequence model directly assists in the necessary verifications because it is formal, precise, and unambiguous. The reliance that can be placed upon the verifications performed for operations based on consequences is as strong as the reliance that can be placed upon the operations composing them and upon the underlying hardware of execution (to paraphrase Hoare quoted in []).
Toolset
-
To assist designers in using ZENO to specify programs, a set of tools is necessary. These tools are not intended to provide an entire design and run-time environment, but are used to add ZENO specifications to Ada programs and then verify properties of the programs. Instead of relying on Ada's exception handling model, a designer can specify an operation's consequences using ZENO and then implement the algorithmic portions of the operations in Ada. The ZENO specifications are embedded in the Ada interface specifications for the packages and subprograms making up the design, and a full program implementation is constructed by putting together the Ada algorithms with the basic structures that implement the properties specified in ZENO notation. The toolset makes this process easier and free of common errors.
-
The toolset includes:
Specification Checker
-
There are a number of properties that must hold for the definition of an operation, or that operation cannot be called ``well-specified'' within the model. These properties have effective algorithms for detecting whether the operation is well-specified or not, and each necessary property is checked before allowing the full Ada implementation of the program to be constructed.
Visualizer
-
A data-flow graph can be constructed from operation specifications. The visualizer produces this graph and displays it on an appropriate graphic display device. The visible data-flow graph is useful for examining the connections and interactions within a design, and for obtaining an overview of a design's structure. Zooming in and out of operations will be supported to allow the entire design to be traversed and inspected. The outermost view depicts an entire non-concurrent program as a single operation, while the lower-level operations contained within it can be individually zoomed into and inspected.
Verifier
-
The verifier attempts to prove that the consequences specified for an upper-level operation are actually implemented by the operations composing it. Using existing proof techniques, the verifier shows that:
the operand space is partitioned by the specification for the operation's outcomes,
-
the operation does not violate its specification by modifying inappropriate operands,
-
the properties of each consequence are guaranteed by the specifications of the operations used to implement that consequence,
-
zones do not observe or modify elements unless they are passed to it in an operand message,
-
zones that are specified as infinitely operating servers are implemented as such, and
-
communication between zones does not degrade due to badly specified message dependencies.
Definitions
Computational Model
-
A member of a data type, where the data type can be composed from other data types. For example,
 .
.
-
A relation between a name and an element. The element is also referred to as the variable's value. A value that is possible for any variable is called "undefined;" this corresponds to the variable's value when the variable's name exists but that name has not yet been associated with an element. Every variable has a storage location where its value is kept.
The collection of threads where a variable's name is visible according to the target language's scoping rules.
A set of variables, e.g. (n → 20, y → "input.dat").
A computational action applied to an environment yielding a possibly different environment.
A finite sequence of operations.
A numerical index (into a program).
A triple containing a program, an execution point and an environment.
A relation between a thread and an execution point within the same thread.
A relation between a sequence of threads and a thread.
A data flow between two operations caused by a program. The "sending" operation is called the predecessor and the "receiving" operation is called the successor.
Discussion of Computational Model Definition
-
This section has set down the definitions for several common programming terms that will be used as the basis for defining the consequence model.
-
The concept of a "program" that is defined here is a simplification of what is commonly considered to be a program, but the definition of a program as a sequence of operations is sufficient for general programs; block structure and other complications can be encoded as a set of operations that transform the program's environment as desired. Programs are commonly encoded in a computer's machine language, which has a structure distinctly resembling a sequence of operations with an environment and an execution point.
-
The definition for data flow points to the fact that a data flow operation's parameters can flow to the operation from numerous other operations. The data flow operation will not "fire" until all of its required parameters are present. Control flow can be seen as a special case of this where only one thread passes the parameters to the operation simultaneously. If a program is executed on a uniprocessor machine, then the interpretation of data flow on this machine is equivalent to control flow.
Consequence Model
-
An variable travelling by data flow to an operation where the operation observes and/or modifies the storage location and/or value of the variable. For example, in the addition expression (a + b), a and b are operands to +. In the assignment statement (c = d), c and d are operands to = and c's contents are modified.
-
A formal predicate logic statement in a formal specification language that is used to describe theoretical properties within the program. For example,
 and
and 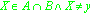 are both characteristic predicates in Z.
are both characteristic predicates in Z.
-
The n-dimensional space generated by the cross-product of an operation's operand types. This is also called the input domain. For example, the operand space for an integer addition operation is the set { Integer × Integer } and contains elements such as (3,5) and (-30, 8).
-
An element computed by an operation that is passed through a connection to a successor. Results are specified using a characteristic predicate. For example, Result ::=
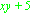 or Result ::=
or Result ::=  . The second example specifies a set containing all elements with the same type as the elements of the sequence N that are not contained in the sequence N at any of the indices listed in a set Q.
. The second example specifies a set containing all elements with the same type as the elements of the sequence N that are not contained in the sequence N at any of the indices listed in a set Q.
-
The discriminated union of a set of results. A member of the result space has a type and value dictated by one member of the set of results.
-
A change to an operand that is described by a characteristic predicate. The operand becomes (or is assigned) the value specified in the predicate. For example,
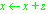 and
and  are both modification statements. From the perspective of the operation, modifications occur at points defined by the source code. From the perspective of the operation's invoker, modifications occur before the operation returns.
are both modification statements. From the perspective of the operation, modifications occur at points defined by the source code. From the perspective of the operation's invoker, modifications occur before the operation returns.
-
The guard on a connection that allows data flow when a characteristic predicate evaluates to TRUE. For example, data would flow on an outcome with a predicate
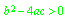 when a=2, b=5, and c=3.
when a=2, b=5, and c=3.
-
A triple containing a result, an outcome, and a set of modifications. The meaning is that when the outcome's specified predicate evaluates to TRUE, then the specified modifications are made before the specified result is passed along the outcome's connection.
-
A computation that: 1) has a specification listing the number and type of all operands, 2) has a specification for all consequences, 3) always concludes with exactly one of the consequences, and 4) has an operand space partitioned by the set of consequences.
-
A relation from an operand space to a result space that is total. The valid or defined domain of the relation is thus equal to the operand space. The preconditions for a total operation are thus just {TRUE}, while the postconditions are partially specified by the consequences. The well-formed consequential operation as defined above is a total operation.
Discussion of Consequence Model
-
<deverbosify>
-
<add block structuring/conseq types/other tasties>
-
<include defense denosem domains in separate appendix?>
-
This section has defined the consequence model. The name consequence has been chosen because it implies a situation that is fully determined by a prior set of conditions. It reaffirms the fact that a specification for an operation should be defined in terms of what the programmer intends to definitely happen when the operation is invoked. This is intended to counteract the connotation of an exception as an unusual or abnormal event; instead, a particular set of consequences is to be expected ahead of time from the specification of the operation.
-
The notion of an operation is recursive. An operation can represent primitive computations provided by a particular programming language or computer, or it can be used to represent complex computations that are composed from multiple lower-level operations. Operations have both a specification and an implementation, although clearly the implementation of some primitive or system operations might not be available for inspection.
-
-------------
-
-
Developing methods for enforcing that operation specifications define a true partition is one of the goals of this research.
flow
-
extend static & dynamic notions to connectivity
anomalies formal definition
control flow model using control point
-
statement of properties in terms of model
-
detection of bad things, proof of good things
-
-
Different outcomes arise because the operand space is naturally or artificially partitioned into equivalence classes. A natural partition is one in which the nature of the data object generates the partition. An artificial partition is one where lower level implementation details (such as hardware support for mathematical operations) cause subsets of the input domain to be differentiated. The equivalence classes categorize the sets of elements that must be treated differently from other sets due to the operation's implementation or due to the definition of the operands. Each outcome might need different treatment by the invoker, and thus each outcome is represented as a separate data flow path leaving the operation.
-
The consequence is the semantic construct in this model that is analogous to the exception. However, the programmer defines consequences more rigorously than exceptions are defined in conventional programming languages. A consequence specification details exactly what an operation accomplishes when it concludes with that consequence by describing the cause of the consequence (the outcome), the service provided by the consequence (the result), and how the parameters are changed when the operation completes (the modifications).
Verification Definitions
A residual fault in a program implementation that can cause the specification for the program to be violated.
A characteristic of a program implementation.
A formal argument that a program possesses a particular property.
The establishment of a set of property proofs for a program.
Discussion of Verification Definitions
Total Stack
-
<deverbosify>
-
This section provides an example of using total operations within the context of an object oriented stack. The disadvantage of showing how to do a stack is that every specification language offers its own version of a stack, but the advantage is that the stack is commonly known and simple to understand.
-
A bounded stack has four axiomatically spannable equivalence classes that will be called empty, full, erroneous, and partially-full (all stacks that are neither full nor empty nor erroneous). The set of axioms is simple in this case:
a stack is full iff the used extent is all slots and forall slots, an element is stored in the slot.
-
a stack is empty iff the used extent is all slots and forall slots, no element is stored in the slot.
-
a stack is erroneous if therexists a slot that is within the used extent of the stack that has no element in it or if therexists a slot that is not within the used extent of the stack that has an element in it or if the counter of the used extent contains an impossible (negative or too large) value.
-
a stack is partially-full iff a) its used extent is less than the whole stack and greater than the empty stack, b) forall used slots, there is an element in the slot and c) for all unused slots, there is no element in the slot.
-
Showing that this set of axioms partitions all stacks requires showing that the abstract representation for a stack is partitioned by the axioms. This is the model for the stack in terms of concepts, rather than in terms of specific software or hardware representations. The abstract representation for a stack is an integer counter and an array of storage locations. The counter represents how many of the storage locations are used starting from the first location and progressing sequentially through the array.
-
Given that the only two components inside a stack object are its counter and its array of elements, then the axioms above partition the stack. An informal proof is that all invalid counters are treated in case 3, and that the cases 1 and 2 are the boundary conditions for valid counters and valid content placements, while case 4 is all middle values between these two extremes for valid counters. Besides treating invalid counters, case 3 also treats all forms of invalid content placement. These content placements have either a hole where an element should be or they have a filled slot that is not supposed to be in use.
-
The abstract representation must also be shown to map to a concrete representation in which the partition also holds. The concrete representation is still quite abstract; the most concrete level addressed here will be an underlying programming language representation of the object in question.
-
<note that content validity not treated...>
-
-
Part of verifying this stack object might be showing that no valid combination of stack operations results in an erroneous stack. The sets of valid stack combinations are where the partial nature of the stack data type comes in, but the operations on the stack are still total operations.
-
Note that the axioms do not prohibit the contents of the stack indices to be wildly different from whatever was stored there, but the result portions of the specifications for the stack consequences can be shown to ensure that the elements are stored appropriately. Given protection of the internal stack data, the contents can be assumed not to change except by the operations defined on the stack.
-
If the set of axioms for combining operations on an object are themselves total, then all uses of the object can be categorized as valid or invalid based on the axioms?
-
-
The theorem set generated by the ??
-
A stack push operation can add an element to an empty stack and to a partially-full stack, it cannot add to a full stack. Thus, the partition for the push operation has two equivalence classes that might be called Full and Non-full, where Non-full incorporates both empty and partially-full. Likewise, a stack pop operation cannot remove an element from an empty stack, but can from the other two kinds. The Pop operation's partition therefore might have two equivalence classes called Empty and Non-empty.
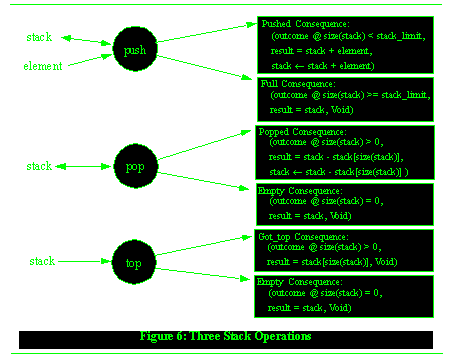
-
The three common operations on stacks are depicted in Figure See Three Stack Operations. The result specifications are based on an array-like notation for a stack. The `+' operator represents a concatenation of the stack and a new element. The `-' operator represents the removal of an element from the stack. The brackets operator extracts a single element from the stack at a particular position. Size is the current number of elements on the stack.
-
These three operations are each total.
-




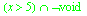 . The error consequence has this `precedence' over the intended consequence specification because the error has a concrete representation while the intended semantics are yet to be proven.
. The error consequence has this `precedence' over the intended consequence specification because the error has a concrete representation while the intended semantics are yet to be proven.

 .
. and
and 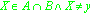 are both characteristic predicates in Z.
are both characteristic predicates in Z.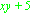 or Result ::=
or Result ::=  . The second example specifies a set containing all elements with the same type as the elements of the sequence N that are not contained in the sequence N at any of the indices listed in a set Q.
. The second example specifies a set containing all elements with the same type as the elements of the sequence N that are not contained in the sequence N at any of the indices listed in a set Q.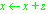 and
and  are both modification statements. From the perspective of the operation, modifications occur at points defined by the source code. From the perspective of the operation's invoker, modifications occur before the operation returns.
are both modification statements. From the perspective of the operation, modifications occur at points defined by the source code. From the perspective of the operation's invoker, modifications occur before the operation returns.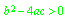 when a=2, b=5, and c=3.
when a=2, b=5, and c=3.